![[MaPhySto logo]](../../Graphics/logo.gif)
Centre for Mathematical Physics and Stochastics
Department of Mathematical Sciences, University of Aarhus
![[MaPhySto logo]](../../Graphics/logo.gif)
The Geometric Mathematical Physics seminar was started in July 1998 as a montly seminar during terms. Since September 1999 it has been running as an integrated half-part of the Department's Topology seminar. Seminars are announced via the Department's local calendar and via the the MatNyt calendar maintained by the Danish Mathematical Society.
The Seminar is organized by Jørgen Ellegaard Andersen.
The talks listed below are within the field of Geometric Mathematical Physics and has therefore been financed by MaPhySto.
Abstract: The Seiberg-Witten invariant of a 3-manifold M is an integer-valued function SW=SW(M) on the set of Spinc-structures on M. It is determined by the Seiberg-Witten invariant of the 4-manifold M x S1. The aim of the talk is to give a combinatorial approach to SW(M) based on the theory of Reidemeister torsions.
Abstract: Gauge theries are dynamical systems whose phase space is the space of connections on a principal bundle. Examples are Yang-Mills theory (of interest in high energy physics) and Chern-Simons theory (of interest in topology). We will show that the gauge invariant observables ( traces of holonomies) satisfy a Poisson algebra with a natural geometric interpretation. We will describe a quantization of this algebra (deformation of the Poisson algebra into an associative algebra). Some ideas on the application of these ideas to topology will be presented at an informal level.
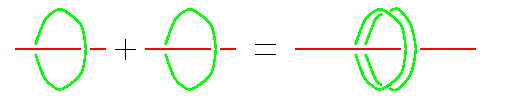
Abstract: One of the earliest demonstrations of the identity 1+1=2 was using the Chinese soroban (abacus). The proof is topological in nature: the number 1 is represented by a rod with a bead on it. The sum 1+1 would be taking two such rods and connecting them end to end, and the result is clearly topologically equivalent to the number 2, represented by a single rod with a double bead on it. In modern language, a ``rod with a bead'' is nothing but the Hopf link, with one of the components cut open, and the identity 1+1=2 becomes ``the connected sum of two cut Hopf Links is equal to a single cut Hopf Link, with its uncut component doubled''.
We apply the Stonehenge machinery to this identity, and get that two big sums of diagrams are equal (modulo some necessary relations). When a Lie algebra is given and these diagrams are interpreted as tensors in certain spaces associated with the Lie algebra, this equality becomes an easy proof of the multiplicativity property of the non-obvious Harish-Chandra-Duflo isomorphism.
The diagram equality we prove and use is the ``Wheeling Conjecture'' of Garoufalidis, Rozansky, D. Thurston and myself, first discovered in Aarhus some three years ago, and, independently, of Deligne. The 1+1=2 proof is due to D. Thurston and myself (Jerusalem, September 1998).
Abstract: The symmetry principle was discovered by Kirby-Melvin for sl2 and by Kohno-Takata for sln. We put the symmetry principle in a simple setting, and discuss a generalisation (for all simple Lie algebras) which says that quantum invariants of links at roots of unity is skew-invariant under the action of the center of the corresponding Lie groups. This leads to the projective version of quantum invariants of 3-manifolds, a finer and better version of quantum invariants. Ohtsuki proved that the projective version of quantum invariants, for the sl2 case, has a perturbative expansion. The result had led him to the definition of finite type invariants of homology 3-spheres. We will discuss the perturbative expansion in general case (for every simple Lie algebra), and explain the relation between the perturbative expansion and the LMO invariant.
Abstract: This talk describes the construction of invariants of rational homology spheres and of knots in a rational homology sphere using configuration space integrals.
In the case of knot invariants, it is shown that - in analogy with the cases when the ambient space is R3 or is a surface cross an interval - it is possible to combine them to yield the (framed) universal Vassiliev invariant.
Abstract: We investigate invariants of hyperkaehler manifolds introduced by Rozansky and Witten -- they associate an invariant to each graph cohomology class. It is obtained by using the graph to perform contractions on a power of the curvature tensor and then integrating the resulting scalar over the manifold. Certain combinations of these invariants give us the Chern numbers. A power of the L2 norm of the curvature of the manifold also appears as one of these invariants (up to rescaling by the volume). Remarkably, a result in knot theory known as the wheeling conjecture gives us certain relations among these invariants and this allows us in particular to express the L2 norm of the curvature in terms of characteristic classes and the volume.
Abstract: In these talks I will talk about finite type invariants and surgery equivalence relations of knots and $3$-manifolds. I introduce ``claspers'', as a useful tool for studying finite type invariants and surgery equivalence relations. We may think of claspers as natural ``topological realizations'' of web diagrams (uni-trivalent graphs). Also, with claspers, we can regard theories of finite type invariants and surgery equivalence relations as a kind of ``commutator calculus in 3-manifolds''.
Abstract: The Futaki Invariant is a Lie algebra character whose non-vanishing obstructs the existence of Kähler metrics of constant scalar curvature in a given Kähler class of a compact manifold. I describe further information extracted from this invariant obstructing the existence of ``harmonic pairs'' of metrics in distinct Kähler classes, as well as an analogous invariant giving obstruction information for the ``central curvature'' of a Kähler metric. The latter invariant is suggested by an interpretation of the theory in terms of (holomorphic) equivariant cohomology. I discuss relevant localization issues in this framework, in part consisting of joint work with Yael Karshon.
Abstract: We will discuss recent work on moduli spaces of vector bundles of rank two on curves. These moduli spaces can be used to define flat connections on certain vector bundles over the moduli space of curves. The holonomy representations of these connections give representations of the mapping class group. We will recall the relation of this connection with Hitchin's Hamiltonian system and we work out the case of genus 2 curves in some detail.
Abstract: Recently, a new definition of the topological charge of a lattice gauge field has been introduced. Unlike previous, rather messy definitions, this one has a mathematically elegant formulation (in terms of the spectral flow of a hermitian Dirac-Wilson operator) and equals the index of an operator on lattice spinor fields -- Neuberger's ``overlap Dirac'' operator. I will discuss recent progress in showing that this lattice index formula reduces in the continuum limit to the index formula for the usual Dirac operator coupled to a gauge field.
Abstract: Vaughan Jones introduced the theory of subfactors in the early 80's as a "Galois theory" for inclusions of certain algebras of operators on a Hilbert space. He showed that these inclusions are extremely rigid and that an amazingly rich combinatorial structure is naturally associated to each subfactor. An interplay of analytical, algebraic-combinatorial and topological techniques is intrinsic to the theory.
A subfactor can be viewed as a group-like object that encodes what one might call generalized symmetries of the mathematical or physical situation from which it was constructed. To decode this information one has to compute a system of inclusions of certain finite dimensional algebras naturally associated to the subfactor. This structure can be described as a planar algebra, that is a graded vector space whose elements are represented by labelled n-boxes which can be combined in planar, but otherwise quite arbitrary ways. A planar algebra comes with a partition function, which is an invariant for planar networks (for instance, the Jones polynomial arises in this way).
I will discuss the notion of planar algebras (introduced recently by Jones) and I will present a number of examples such as the Temperley-Lieb and the Fuss-Catalan algebras, discovered by Jones and myself.
Abstract: The Verlinde formula arose originally in physics as the dimension of the space of so-called `conformal blocks' associated to a complex curve (or Riemann surface). The talk will begin by presenting two related, but purely mathematical, approaches, one algebro-geometrical, and one from `quantum topology'. I will then discuss recent joint work with J. E. Andersen on a natural action of a finite Heisenberg group on the Verlinde vector spaces, which leads to various refinements of the Verlinde formula.
Abstract: For manifolds with boundaries, indices of Dirac operators with Atiyah-Patodi-Singer boundary conditions give invariants of manifolds with boundaries, which behave additively under gluing of manifolds along common boundaries, provided that they are correctly normalized. The boundary correction term is the $\eta$-invariant, which changes sign under change of orientation, and therefore cansels out under gluing of manifolds. On the other hand the Wall non-additivity formula for the signature from 1969 shows that new phenomena happen when one passes from index invariants on manifolds with boundary to the corresponding invariants for manifolds with corners of codimension 2. However, in particular in higher codimension, not much is known about how to define index invariants, or which correction terms appear in gluing formulas.
I will give some partial answers to the above. First I will give a generalization of the Atiyah-Patodi-Singer boundary conditions for a manifold with corners of codimenison 2. This gives a new proof of the Gauss-Bonnet theorem for manifolds with corners of codimension 2 as well as a new version of the signature formula for manifolds with corners and a more general index theorem corresponding to the local twisted spin complex, which covers a lot of cases not covered by other approaches.
In the second part of the talk I will give a geometric construction, which gives a proof of the splitting formula for $\eta$-invariants of manifolds with wedge singularities into $\eta$-invariants of manifolds with corners. The proof uses index theory for manifolds with corners of codimension 3 corresponding to the theory in codimension 2, which is explained in the first part.
Abstract: We apply the idea of a topological quantum field theory (TQFT) to maps from manifolds into topological spaces. This leads to a notion of a (d+1)-dimensional homotopy quantum field theory (HQFT) which may be described as a TQFT for closed d-dimensional manifolds and (d+1)-dimensional cobordisms endowed with homotopy classes of maps intoa given space. For a group $\pi$, we introduce cohomological HQFT's with target $K(\pi,1)$ derived from cohomology classes of $\pi$ and its subgroups of finite index. The main body of the paper is concerned with (1+1)-dimensional HQFT's. We classify them in terms of so called crossed group-algebras. In particular, the cohomological (1+1)-dimensional HQFT's over a field of characteristic 0 are classified by simple crossed group-algebras. We introduce two state sum models for (1+1)-dimensional HQFT's and prove that the resulting HQFT's are direct sums of rescaled cohomological HQFT's. We also discuss a version of the Verlinde formula in this setting.
Abstract: We formulate Yang-Mills theory in terms of the large-N limit, viewed as a classical limit, of gauge-invariant dynamical variables, which are closely related to Wilson loops, via deformation quantization. We obtain a Poisson algebra of these dynamcial variables correponding to normal-ordered quantum (at a finite value of Planck's constant) operators. Comparing with a Poisson algebra derived earlier for Weyl-ordered quantum operators, we find, using ideas closely related to topological graph theory, that these two Poisson algebras are, roughly speaking, the same. More precisely speaking, there exists an invertible Poisson morphism between them.
Abstract: This will be an informal seminar on a certain approach to various 3-manifold invariants. The approach is via physics. I will try to explain why physics implies that the invariants in the title are closely related. More concretely the Rozansky-Witten invariants for a compact 3-manifold M with $b_{1}(M) > 0$ are examples of the universal LMO invariant (this is conjectured to be the case for $b_{1}=0$ as well). Some questions regarding the position of the Casson invariant in this scheme of things will also be addressed.
Abstract: In the last decade solutions to many topological or geometrical problems were found with the help of various perturbative quantum field theories. The examples include, e.g., Chern-Simons integral formulas for invariants of links and 3-manifolds and Kontsevich's quantization of Poisson structures. The answer is usually given as a power series of graphs, with each coefficient being a complicated integral over some configuration space associated to a graph. In my talk I will try to explain the meaning of these integrals in a classical topological terms as degrees of certain maps.
Abstract: Gerbes are higher analogues of line bundles and can be described in various ways. I will characterize gerbes-with-connection on a manifold as certain functors on the two-dimensional cobordism category of the manifold. This will allow me to relate flat gerbes to Turaev's definition of 1+1 dimensional homotopy quantum field theories.
Abstract: The complex-valued Quantum Hyperbolic Invariants (QHI) are defined for pairs: (compact closed oriented 3-manifold W, link L in W), and they depend on a flat principal bundle over W whose structural group is a Borel subgroup of SL(2,C). The QHI are constructed using the quantum dilogarithm function, by means of state sum formulas over triangulations "decorated" with (very rich) geometric extra-structures. In the first lecture, we shall define these triangulations and the notion of transit of the extra-structures when the triangulation changes. In the second lecture, we shall concentrate on the definition of the QHI and of a new "dilogarithmic invariant" R based on the classical Rogers dilogarithm and supported by the same kind of decorated triangulations. Then we shall present a so-called "volume conjecture", that would express the dominant term of the asymptotic behaviour of the QHI in terms of R, thus being a classical counterpart to the former.
Abstract: This talk is based on joint work with Yuri Manin. We recover some classical arithmetic information on modular curves, such as modular symbols and the modular complex, Dirichlet series related to modular forms of weight 2 and the Selberg zeta function, in terms of a `boundary' PGL(2,Z)\PGL(2,R) (to be regarded as a noncommutative space) and a dynamical system related to the shift of the continued fraction expansion.
Abstract: Abstract: p-compact groups and p-local finite groups are p-local homotopy theoretic analogs of compact (connected) Lie groups and finite groups respectively. The recently completed classification of p-compact groups, p odd, states that connected p-compact groups are in 1-1 correspondence with finite reflection groups over the p-adic integers, ie a classification completely analogous to the classification of compact Lie groups. It is natural to speculate whether simple p-local finite groups should admit a classification analogous to the classification of finite simple group. In joint work with Broto, Castellana, Levi, and Oliver we examine the first steps, and try to build the relevant extension theory. My talk will be an exposition of this work.