![[MaPhySto logo]](../../Graphics/logo.gif)
The Geometric Mathematical Physics seminar was started in July 1998 as a montly seminar during terms at the Department of Mathematical Sciences, University of Aarhus. Since September 1999 it has been running as an integrated half-part of the Department's Topology seminar. Seminars are announced via MaPhySto's calender, the Department's local calendar and via the the MatNyt calendar maintained by the Danish Mathematical Society.
The Seminar is organized by Jørgen Ellegaard Andersen.
The talks listed below are within the field of Geometric Mathematical Physics and has therefore been financed by MaPhySto.
Abstract: We will construct modular categories from SU(N) specializations
of Homfly skein theory at roots of unity, and compute
the corresponding Verlinde formula.
This lecture is part of the course "TQFT and Knot theory".
Abstract: A modular category is a braided category with some additional
algebraic features.
The interest of this concept is that it provides
a Topological Quantum Field Theory in dimension 3.
The Verlinde formulas associated with a modular category are the
dimension of the TQFT modules.
We discuss reductions and refinements of these formulas for
modular categories related with SU(N).
Our main result is a splitting of the Verlinde formula,
corresponding to a brick decomposition of the TQFT modules
whose summands are indexed by spin structures modulo
an even integer.
We introduce the notion of a spin modular category, and state the
decomposition theorem in this general context.
Abstract: The Homfly invariant of a link is a two variable
polynomial with specializations corresponding to the
so-called SU(N) quantum invariant.
We will present the corresponding skein theory,
and construct a semisimple ribbon category out of it.
The key point here is the structure of Hecke algebras.
This lecture is part of the course "TQFT and Knot theory".
Abstract: Property P for knots is concerned with the question of constructing
counterexamples to the Poincaré conjecture by surgery on the 3-sphere
along a single knot. The talk reviews the recent work by Kronheimer on
Mrowka on this question, with special emphasis on the role played by
contact geometry.
Abstract: In this talk we give an introduction to Seiberg-Witten theory on 3-manifolds based on the work of Y. Lim [Seiberg-Witten invariants for 3-manifolds in the case b_1=0 or 1, Pacific J. Math. 195 (2000)] and W. Chen [Casson's invariant and Seiberg-Witten gauge theory, Turkish J. Math. 21 (1997)]. The Seiberg-Witten equations are interpreted as critical point equations of the Chern-Simons-Dirac functional. Viewing the latter as a Morse function, we define the Seiberg-Witten invariant as the Euler characteristic of the configuration space modulo gauge equivalence. We then analyse its behaviour under deformation of the Riemannian metric in order to obtain a topological invariant. For rational homology spheres, this can only be achieved by modifying the Seiberg-Witten invariant by a combination of eta-invariants.
Abstract: I will describe joint work with Paul Seidel which defines an
invariant of oriented links in the three-sphere by combining ideas from the
algebraic geometry of Lie algebras with Lagrangian Floer homology. We
conjecture that the invariant is a geometric model for Mikhail Khovanov's
combinatorially defined homology groups.
Abstract: I will give a combinatorial description of closed curves on surfaces
in terms of certain permutations called charts. Automorphisms of curves will be
described in terms of charts and then the total number of topological types of
curves will be computed. At the end I will discuss relations between charts,
curves, words, and complex structures on surfaces.
Abstract: A geometric construction that creates a knotted codimension
2 submanifold in S^2n-1 from a selfindexing Morse function on D^n will
be presented.
Abstract: The theory of toric varieties provides a fruitful link between combinatorial
questions on convex polytopes and algebraic geometry. For example there is
a beautiful characterization of the possible numbers of faces
of a simplicial convex polytope due to P. McMullen, L. Billera, C. Lee and
R. Stanley. Stanley could prove the necessity of the conditions by translating
them into topological statements on the projective toric variety associated
to the polytope.
In this talk, I will consider polytopes with a central symmetry, but
not necessarily simplicial, and prove a lower bound for a certain combinatorial
invariant, using intersection cohomology.
Abstract: We will discuss some structural properties of the
"Integral TQFT" constructed in joint work with Pat Gilmer.
Abstract: A virtual string is a scheme of self-intersections of a closed curve
on a surface. We study algebraic invariants of virtual strings as well as two
equivalence relations on the set of strings: homotopy and cobordism.
We also discuss connections between virtual strings and virtual knots
Abstract: I will discuss a conjecture mainly due to Garoufalidis,
Gelca, and Frohman about the relations between the colored Jones
polynomial and the A-polynomial of a knot. I will show some partial
results for 2-bridge knots using the calculation of the Kauffman bracket skein module of knot complements.
Abstract: The Seifert surface is a well-known and very useful tool in link theory. For
instance, it permits to study the Alexander invariants, the Conway polynomial,
and the signature of an oriented link. In this talk, we shall introduce
'generalized Seifert surfaces' for colored links. They provide a geometric
interpretation of the multivariable Alexander invariants and the Conway
potential function. They also make it possible to define a multivariable
signature that generalizes the Levine-Tristarm signature.
Abstract: Recent results about the existence and nonexistence of solitons in
noncommutative spaces are reviewed. We also discuss the existence theory
for nonlinear noncommutative waves and show that the propagation
velocity is infinite
Abstract: We will describe joint work with Gregor Masbaum where we find
explicit
bases for abstractly defined lattices ( over Z[zeta_p] ) in the vector
space over Q[zeta_p] associated to surfaces by the SO(3) TQFT at an odd
prime p. We take a skein theory approach.
Abstract: For construction of invariants for families of bundles, integration along
the fiber is usually applied in order to obtain forms defined on the
parameter space. In the case of families of bundles with connection the
classical Chern-Weil theory gives rise to invariants living in smooth
Deligne cohomology, and hence a notion of integration along the fiber is
needed in this setting. We present two constructions of such a map: One
defined in the simplicial model for Deligne cohomology introduced by Dupont
and Kamber and another defined in a more combinatorial model associated to a
triangulation of the bundle.
Abstract:
Let X be a compact Riemann surface of genus greater than or equal to 2.
The semistable holomorphic vector bundles on X of rank n and determinant
L are parametrised by the moduli space M(n,L). The Picard group of M(n,L)
is isomorphic to Z with a unique ample generator K(n,L). The spaces Z_k(n,L)
of holomorphic sections in the k'th tensor power of K(n,L) have been studied
intensely, due to their central role in the gauge-theoretic approach to 2+1
dimensional TQFT.
There is a natural action on M(n,L) of the group J^(n)(X) of n-torsion points
in the Jacobian of X, gotten by tensoring with the corresponding line bundles.
I define certain lifts of this action to K(n,L) (and hence to Z_k(n,L) and give
a presentation of the group generated by such lifts. In the proces, a detailed
study of the fixed point varieties for the action of J^(n)(X) on M(n,L) becomes
necessary.
Abstract: This talk will be an introduction to a homology theory
of links, invented by Mikhail Khovanov in 1999. It associates to every
link diagram a bigraded chain complex whose graded Euler characteristic
is the Jones polynomial. The chain complex is invariant up to chain
equivalence under Reidemeister moves, so the isomorphism classes
of the associated homology groups are link invariants. These invariants
are stronger than the Jones polynomial. Also, Khovanov homology is
a functor. Namely, any link cobordism induces a homomorphism between the
homology groups of its boundary links, which is invariant (up to sign)
under ambient isotopy of the link cobordism. This latter statement
comes with an important caveat, which also will be mentioned in the talk,
if time permits.
Abstract: The motivation for studying Yang Mills matrix integrals comes
from string theory but they present many interesting mathematical problems
which can be studied in their own right. I will explain very qualitatively
what the
string theory connection is. The integrals are essentially a measure, not
all of whose
moments are finite; I will discuss the convergence properties both for the
bosonic case
and the supersymmetric one. Lastly I will discuss the properties of the
Polyakov line.
Abstract: A hyperKahler manifold with torsion (HKT manifold) is a
hyperhermitian manifold together with a hyperhermitian connexion whose torsion is totally antisymmetric. We will explain how one can generalize the not on of Kahler potential on HKT manifolds and we will show that such a potential always exists locally
Abstract: I will discuss a mathematical formulation of a
very special case of entanglement. This formulation poses a
geometrical question, namely the determination of a
certain convex cone in the real vectorspace of
Hermitian matrices. I study this space using Grassman
spaces and algebraic group actions.
Abstract: The work presented in this talk is joint with Toshie Takata.
I will first present compact expressions for a certain family
of representations $R_{r}^{frg}$ indexed by a complex finite
dimensional simple Lie algebra $frg$ and a positive integer $r$ bigger than or equal to the dual coxeter number of $frg$
(the so-called shifted quantum level).
These expressions are obtained using a certain (multidimensional)
reciprocity formula together with certain symmetries.
The representations $R_{r}^{frg}$ are known from
the study of theta functions and modular forms in connection with the study of affine Lie algebras. They also play a fundamental role in conformal field theory and thereby in the Chern--Simons path integral TQFT's of Witten.
I will explain how these representations enter surgery fomulas
for the rigorously defined quantum invariants of $3$--manifolds, the so-called
Reshetikhin--Turaev invariants. In the final part of the talk I will pay
special attention to the Seifert manifolds. I will present compact
expressions for the quantum invariants of these spaces using our expressions
for the representations $R_{r}^{frg}$. In particular, we obtain hereby
a formula for the large $r$ asymptotic expansion of the quantum invariants
of lens spaces. This result is in accordance with the asymptotic expansion
conjecture of J.E.Andersen. If time permits I will explain some of
the problems encountered when trying to calculate these asymptotics for more
general Seifert manifolds.
Abstract: A Riemannian manifold with upper curvature bound 1
is said to have positive spherical rank if any geodesic
$c$ has a conjugate point at $pi$.
It is easy to see that this notion is analogous
to the notions of Euclidean and hyperbolic rank for manifolds
with upper curvature bound 0 and -1, respectively.
In a joint work with Krishnan Shankar and Ralf Spatzier we
prove that a manifold with positive spherical rank is locally
symmetric.
Abstract: It will be explained how to derive a wide class of classical integrable systems (the so-called Hitchin systems) starting with a simplified version of the Chern-Simons theory. These theories are described by the Hamiltonian systems defined on the Higgs bundles over Riemann curves.
The Lax representation, conservation laws, spectral
curves and the action-angle variables are the natural ingredients of this construction. The case of the genus one curves will be elaborated in details.
It leads to the integrable many-body problem of Calogero-Moser type and to the integrable elliptic tops related to generalized XYZ spin chains.
Abstract: In the talk will be discussed the Voronoi's theory of perfect lattices in an Euclidian space of the dimension n,describing a nice triangulation of the classifying space for the group SL(n,Z).
Perfect lattices give local maxima of density for the corresponding sphere packings.Spherical designs are combinatorial structures important in applied mathematics.In the talk there will be considered interrelations of these to
topics.In some cases the interralation can be explained by modular forms.
Abstract: We discuss the definition of both crossed group
coalgebras and crossed group categories introduced by
Turaev for topological motivation. The first is a
generalisation of the standard notion of a Hopf
algebra, the second of a tensor category.
Quasitrinagular structures have an analog in this
context.
For crossed group coalgebras, we provide an analog of
Drinfeld quantum double construction. In that way,
starting from a crossed coalgebra H, we obtain a
quasitriangular crossed coalgebra D(H).
For crossed group categories, we provide an analog of
Drinfeld and Joyal - Street center construction:
starting from a crossed category C, we obtain a
braided crossed category Z(C).
We consider the case C=Rep(H). By introducing the
category YD(H) of Yetter-Drinfeld modules over H, we
prove the isomorphism Rep(D(H))=YD(H)=Z(Rep(H)).
Abstract: On an arbitrary almost-Kähler manifold,
starting from a natural
affine connection with nontrivial torsion
which respects the
almost-Kähler structure, in joint work with
A. Karabegov a Fedosov-type deformation quantization
on this manifold was constructed.
This talk reports on the result and
supplies an overview of the essential steps in the
construction.
On this way Fedosov's geometric
method to obtain a deformation quantization is explained.
Abstract: Quantum averages of the Wilson loops (holonomies) are calculated
in gauge theory on a noncommutative plane using a path-integral
representation of the star products.
It is shown how the stringy representation of two-dimensional
Yang-Mills theory is reproduced at large parameter of noncommutativity
Abstract: Habiro has shown using quantum groups that the colored Jones polynomial
of a knot has a so-called cyclotomic expansion. This expansion is useful
for studying the volume conjecture. It is also an important tool for
constructing Habiro's universal $fsl_2$ invariant of integral homology
$3$-spheres. Explicit computations of this expansion, however, existed only
for a few knots.
In this talk I will explain how to use skein theory to compute the cyclotomic
expansion for twist knots. This is an infinite series of knots including
the trefoil and the figure eight knot, and my formulas generalize previously
known formulas of Habiro and Le for those two knots.
Abstract: The tame symbol associated to a pair of invertible holomorphic
functions can be computed as a cup product in Deligne
cohomology. This construction produces a line bundle equipped
with an analytic connection. "Higher" versions were considered by
Brylinski and McLaughlin and related to gerbes (or 2-gerbes)
equipped with an appropriate notion of connective structure.
These constructions can be enhanced to take into account the
datum of a hermitian structure---the resulting complexes
(resp. cohomology) are termed Hermitian-holomorphic Deligne (HHD)
complexes (resp. cohomology). As a simple example, the group of
isomorphism classes of holomorphic line bundles with hermitian
metric is expressed as a degree 2 (hyper)cohomology group with
values in one of the HHD complexes.
After reviewing the main definitions, we show how these objects
naturally appear in uniformization problems concerning constant
negative curvature metrics on compact Riemann surfaces. One such
metric subordinated to a given conformal structure satisfies an
extremum condition. We present an algebraic construction for the
appropriate functional as the square of the metrized holomorphic
tangent bundle in an HHD group. For a pair of line bundles on a
Riemann surface, this construction recovers the algebraic
approach to the determinant of cohomology.
Abstract: With the method of geometric quantization of Kostant and Souriau, we can associate to a compact prequantizable Kähler manifold a quantum space.
The first applications of this construction were in group theory. More recently, the works of Zelditch and Borthwick-Paul-Uribe have shown that this quantization has good semi-classical properties. As instance, we can define in this setting a semi-classical algebra. It consists of the so-called ``Berezin-Toeplitz operators'', which present many similarities with the pseudo-differential operators. The talk will be devoted to the spectral properties of these operators, such as the estimate of the spectral density and the Bohr-Sommerfeld conditions.
Abstract: Abstract: p-compact groups and p-local finite groups are p-local homotopy theoretic analogs of compact (connected) Lie groups and finite groups respectively. The recently completed classification of p-compact groups, p odd, states that connected p-compact groups are in 1-1 correspondence with finite reflection groups over the p-adic integers, ie a classification completely analogous to the classification of compact Lie groups. It is natural to speculate whether simple p-local finite groups should admit a classification analogous to the classification of finite simple group. In joint work with Broto, Castellana, Levi, and Oliver we examine the first steps, and try to build the relevant extension theory. My talk will be an exposition of this work.
Abstract: This talk is based on joint work with Yuri Manin. We recover some classical arithmetic information on modular curves, such as modular symbols and the modular complex, Dirichlet series related to modular forms of weight 2 and the Selberg zeta function, in terms of a `boundary' PGL(2,Z)PGL(2,R) (to be regarded as a noncommutative space) and a dynamical system related to the shift of the continued fraction expansion.
Abstract: The complex-valued Quantum Hyperbolic Invariants (QHI) are defined for pairs: (compact closed oriented 3-manifold W, link L in W), and they depend on a flat principal bundle over W whose structural group is a Borel subgroup of SL(2,C). The QHI are constructed using the quantum dilogarithm function, by means of state sum formulas over triangulations "decorated" with (very rich) geometric extra-structures. In the first lecture, we shall define these triangulations and the notion of transit of the extra-structures when the triangulation changes. In the second lecture, we shall concentrate on the definition of the QHI and of a new "dilogarithmic invariant" R based on the classical Rogers dilogarithm and supported by the same kind of decorated triangulations. Then we shall present a so-called "volume conjecture", that would express the dominant term of the asymptotic behaviour of the QHI in terms of R, thus being a classical counterpart to the former.
Abstract: Gerbes are higher analogues of line bundles and can be described in various ways. I will characterize gerbes-with-connection on a manifold as certain functors on the two-dimensional cobordism category of the manifold. This will allow me to relate flat gerbes to Turaev's definition of 1+1 dimensional homotopy quantum field theories.
Abstract: In the last decade solutions to many topological or geometrical problems were found with the help of various perturbative quantum field theories. The examples include, e.g., Chern-Simons integral formulas for invariants of links and 3-manifolds and Kontsevich's quantization of Poisson structures. The answer is usually given as a power series of graphs, with each coefficient being a complicated integral over some configuration space associated to a graph. In my talk I will try to explain the meaning of these integrals in a classical topological terms as degrees of certain maps.
Abstract: This will be an informal seminar on a certain approach to various 3-manifold invariants. The approach is via physics. I will try to explain why physics implies that the invariants in the title are closely related. More concretely the Rozansky-Witten invariants for a compact 3-manifold M with $b_{1}(M) > 0(NULL) are examples of the universal LMO invariant (this is conjectured to be the case for $b_{1}=0(NULL) as well). Some questions regarding the position of the Casson invariant in this scheme of things will also be addressed.
Abstract: We formulate Yang-Mills theory in terms of the large-N limit, viewed as a classical limit, of gauge-invariant dynamical variables, which are closely related to Wilson loops, via deformation quantization. We obtain a Poisson algebra of these dynamcial variables correponding to normal-ordered quantum (at a finite value of Planck's constant) operators. Comparing with a Poisson algebra derived earlier for Weyl-ordered quantum operators, we find, using ideas closely related to topological graph theory, that these two Poisson algebras are, roughly speaking, the same. More precisely speaking, there exists an invertible Poisson morphism between them.
Abstract: We apply the idea of a topological quantum field theory (TQFT) to maps from manifolds into topological spaces. This leads to a notion of a (d+1)-dimensional homotopy quantum field theory (HQFT) which may be described as a TQFT for closed d-dimensional manifolds and (d+1)-dimensional cobordisms endowed with homotopy classes of maps intoa given space. For a group (NULL)pi(NULL), we introduce cohomological HQFT's with target $K(pi,1)(NULL) derived from cohomology classes of (NULL)pi(NULL) and its subgroups of finite index. The main body of the paper is concerned with (1+1)-dimensional HQFT's. We classify them in terms of so called crossed group-algebras. In particular, the cohomological (1+1)-dimensional HQFT's over a field of characteristic 0 are classified by simple crossed group-algebras. We introduce two state sum models for (1+1)-dimensional HQFT's and prove that the resulting HQFT's are direct sums of rescaled cohomological HQFT's. We also discuss a version of the Verlinde formula in this setting.
Abstract: For manifolds with boundaries, indices of Dirac operators with Atiyah-Patodi-Singer boundary conditions give invariants of manifolds with boundaries, which behave additively under gluing of manifolds along common boundaries, provided that they are correctly normalized. The boundary correction term is the (NULL)eta(NULL)-invariant, which changes sign under change of orientation, and therefore cansels out under gluing of manifolds. On the other hand the Wall non-additivity formula for the signature from 1969 shows that new phenomena happen when one passes from index invariants on manifolds with boundary to the corresponding invariants for manifolds with corners of codimension 2. However, in particular in higher codimension, not much is known about how to define index invariants, or which correction terms appear in gluing formulas.
I will give some partial answers to the above. First I will give a generalization of the Atiyah-Patodi-Singer boundary conditions for a manifold with corners of codimenison 2. This gives a new proof of the Gauss-Bonnet theorem for manifolds with corners of codimension 2 as well as a new version of the signature formula for manifolds with corners and a more general index theorem corresponding to the local twisted spin complex, which covers a lot of cases not covered by other approaches.
In the second part of the talk I will give a geometric construction, which gives a proof of the splitting formula for (NULL)eta(NULL)-invariants of manifolds with wedge singularities into (NULL)eta(NULL)-invariants of manifolds with corners. The proof uses index theory for manifolds with corners of codimension 3 corresponding to the theory in codimension 2, which is explained in the first part.
Abstract: The Verlinde formula arose originally in physics as the dimension of the space of so-called `conformal blocks' associated to a complex curve (or Riemann surface). The talk will begin by presenting two related, but purely mathematical, approaches, one algebro-geometrical, and one from `quantum topology'. I will then discuss recent joint work with J. E. Andersen on a natural action of a finite Heisenberg group on the Verlinde vector spaces, which leads to various refinements of the Verlinde formula.
Abstract: Vaughan Jones introduced the theory of subfactors in the early 80's as a "Galois theory" for inclusions of certain algebras of operators on a Hilbert space. He showed that these inclusions are extremely rigid and that an amazingly rich combinatorial structure is naturally associated to each subfactor. An interplay of analytical, algebraic-combinatorial and topological techniques is intrinsic to the theory.
A subfactor can be viewed as a group-like object that encodes what one might call generalized symmetries of the mathematical or physical situation from which it was constructed. To decode this information one has to compute a system of inclusions of certain finite dimensional algebras naturally associated to the subfactor. This structure can be described as a planar algebra, that is a graded vector space whose elements are represented by labelled n-boxes which can be combined in planar, but otherwise quite arbitrary ways. A planar algebra comes with a partition function, which is an invariant for planar networks (for instance, the Jones polynomial arises in this way).
I will discuss the notion of planar algebras (introduced recently by Jones) and I will present a number of examples such as the Temperley-Lieb and the Fuss-Catalan algebras, discovered by Jones and myself.
Abstract: Recently, a new definition of the topological charge of a lattice gauge field has been introduced. Unlike previous, rather messy definitions, this one has a mathematically elegant formulation (in terms of the spectral flow of a hermitian Dirac-Wilson operator) and equals the index of an operator on lattice spinor fields -- Neuberger's ``overlap Dirac'' operator. I will discuss recent progress in showing that this lattice index formula reduces in the continuum limit to the index formula for the usual Dirac operator coupled to a gauge field.
Abstract: We will discuss recent work on moduli spaces of vector bundles of rank two on curves. These moduli spaces can be used to define flat connections on certain vector bundles over the moduli space of curves. The holonomy representations of these connections give representations of the mapping class group. We will recall the relation of this connection with Hitchin's Hamiltonian system and we work out the case of genus 2 curves in some detail.
Abstract: The Futaki Invariant is a Lie algebra character whose non-vanishing obstructs the existence of Kähler metrics of constant scalar curvature in a given Kähler class of a compact manifold. I describe further information extracted from this invariant obstructing the existence of ``harmonic pairs'' of metrics in distinct Kähler classes, as well as an analogous invariant giving obstruction information for the ``central curvature'' of a Kähler metric. The latter invariant is suggested by an interpretation of the theory in terms of (holomorphic) equivariant cohomology. I discuss relevant localization issues in this framework, in part consisting of joint work with Yael Karshon.
Abstract: In these talks I will talk about finite type invariants and surgery equivalence relations of knots and $3(NULL)-manifolds. I introduce ``claspers'', as a useful tool for studying finite type invariants and surgery equivalence relations. We may think of claspers as natural ``topological realizations'' of web diagrams (uni-trivalent graphs). Also, with claspers, we can regard theories of finite type invariants and surgery equivalence relations as a kind of ``commutator calculus in 3-manifolds''.
Abstract: We investigate invariants of hyperkaehler manifolds introduced by Rozansky and Witten -- they associate an invariant to each graph cohomology class. It is obtained by using the graph to perform contractions on a power of the curvature tensor and then integrating the resulting scalar over the manifold. Certain combinations of these invariants give us the Chern numbers. A power of the L2 norm of the curvature of the manifold also appears as one of these invariants (up to rescaling by the volume). Remarkably, a result in knot theory known as the wheeling conjecture gives us certain relations among these invariants and this allows us in particular to express the L2 norm of the curvature in terms of characteristic classes and the volume.
Abstract: This talk describes the construction of invariants of rational homology spheres and of knots in a rational homology sphere using configuration space integrals.
In the case of knot invariants, it is shown that - in analogy with the cases when the ambient space is R3 or is a surface cross an interval - it is possible to combine them to yield the (framed) universal Vassiliev invariant.
Abstract: The symmetry principle was discovered by Kirby-Melvin for sl2 and by Kohno-Takata for sln. We put the symmetry principle in a simple setting, and discuss a generalisation (for all simple Lie algebras) which says that quantum invariants of links at roots of unity is skew-invariant under the action of the center of the corresponding Lie groups. This leads to the projective version of quantum invariants of 3-manifolds, a finer and better version of quantum invariants. Ohtsuki proved that the projective version of quantum invariants, for the sl2 case, has a perturbative expansion. The result had led him to the definition of finite type invariants of homology 3-spheres. We will discuss the perturbative expansion in general case (for every simple Lie algebra), and explain the relation between the perturbative expansion and the LMO invariant.
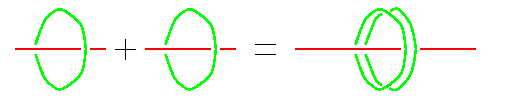
Abstract: One of the earliest demonstrations of the identity 1+1=2 was using the Chinese soroban (abacus). The proof is topological in nature: the number 1 is represented by a rod with a bead on it. The sum 1+1 would be taking two such rods and connecting them end to end, and the result is clearly topologically equivalent to the number 2, represented by a single rod with a double bead on it. In modern language, a ``rod with a bead'' is nothing but the Hopf link, with one of the components cut open, and the identity 1+1=2 becomes ``the connected sum of two cut Hopf Links is equal to a single cut Hopf Link, with its uncut component doubled''.
We apply the Stonehenge machinery to this identity, and get that two big sums of diagrams are equal (modulo some necessary relations). When a Lie algebra is given and these diagrams are interpreted as tensors in certain spaces associated with the Lie algebra, this equality becomes an easy proof of the multiplicativity property of the non-obvious Harish-Chandra-Duflo isomorphism.
The diagram equality we prove and use is the ``Wheeling Conjecture'' of Garoufalidis, Rozansky, D. Thurston and myself, first discovered in Aarhus some three years ago, and, independently, of Deligne. The 1+1=2 proof is due to D. Thurston and myself (Jerusalem, September 1998).
Abstract: Gauge theries are dynamical systems whose phase space is the space of connections on a principal bundle. Examples are Yang-Mills theory (of interest in high energy physics) and Chern-Simons theory (of interest in topology). We will show that the gauge invariant observables ( traces of holonomies) satisfy a Poisson algebra with a natural geometric interpretation. We will describe a quantization of this algebra (deformation of the Poisson algebra into an associative algebra). Some ideas on the application of these ideas to topology will be presented at an informal level.
Abstract: The Seiberg-Witten invariant of a 3-manifold M is an integer-valued function SW=SW(M) on the set of Spinc-structures on M. It is determined by the Seiberg-Witten invariant of the 4-manifold M x S1. The aim of the talk is to give a combinatorial approach to SW(M) based on the theory of Reidemeister torsions.